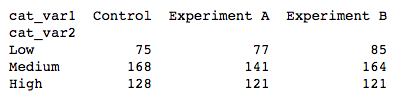Categorical Variable Analysis

Clustered Bar Charts

To depict the relationship between two categorical variables, we can extend the univariate bar chart seen in the previous lesson into a clustered bar chart. Like a standard bar chart, we still want to depict the count of data points in each group, but each group is now a combination of labels on two variables. So we want to organize the bars into an order that makes the plot easy to interpret. In a clustered bar chart, bars are organized into clusters based on levels of the first variable, and then bars are ordered consistently across the second variable within each cluster. This is easiest to see with an example, using seaborn's countplot function. To take the plot from univariate to bivariate, we add the second variable to be plotted under the "hue" argument:

sb.countplot(data = df, x = 'cat_var1', hue = 'cat_var2')

The first categorical variable is depicted by broad x-position (Control, Experiment A, Experiment B). Within each of these groups, three bars are plotted, one for each level of the second categorical variable (Low, Medium, High). Color differentiates each level, and is documented with the legend in the upper-right corner of the plot. The plot tells us that the three "cat_var1" groups are fairly balanced in frequencies across the "cat_var2" levels, though the "Experiment A" group appears to have slighly lower counts of "Medium" points (orange central bar) compared to the other two groups.

The legend position in this example is a bit distracting, however. We can use an Axes method to set the legend properties on the Axes object returned from countplot.

ax = sb.countplot(data = df, x = 'cat_var1', hue = 'cat_var2')
ax.legend(loc = 8, ncol = 3, framealpha = 1, title = 'cat_var2')

(Documentation: Axes.legend)

Alternative Approach (Heat Map)

One alternative way of depicting the relationship between two categorical variables is through a heat map. Heat maps were introduced earlier as the 2-d version of a histogram; here, we're using them as the 2-d version of a bar chart. The seaborn function heatmap is at home with this type of heat map implementation, but the input arguments are unlike most of the visualization functions that have been introduced in this course. Instead of providing the original dataframe, we need to summarize the counts into a matrix that will then be plotted.

ct_counts = df.groupby(['cat_var1', 'cat_var2']).size()
ct_counts = ct_counts.reset_index(name = 'count')
ct_counts = ct_counts.pivot(index = 'cat_var2', columns = 'cat_var1', values = 'count')

(Documentation: Series reset_index, DataFrame pivot)

sb.heatmap(ct_counts)

The heat map tells the same story as the clustered bar chart: the similar colors across the rows suggests that the "cat_var1" group sizes are similarly sized and distributed similarly across levels of "cat_var2". The Experiment A has slightly fewer counts of Medium-level observations, while Control has higher counts of High data points and Experiment B has slightly higher counts of Low points. Compared to the clustered bar chart, however, there is less precision interpreting the magnitude of differences. For this reason, we might want to add annotations to the plot to report counts within each cell.

sb.heatmap(ct_counts, annot = True, fmt = 'd')

annot = True makes it so annotations show up in each cell, but the default string formatting only goes to two digits of precision. Adding fmt = 'd' means that annotations will all be formatted as integers instead. You can use fmt = '.0f' if you have any cells with no counts, in order to account for NaNs.